distortion correction - conformal perspective
- WSH303
Please Log in or Create an account to join the conversation.
Try if it works for youWSH303 wrote: Quick question, lets say I have a curved screen, do I still need this shared to correct perspective?
But technically speaking Yes. More curved the display, more spatial sensation this perspective would give.
Like in this example:
To be correct, if projector would be behind your seat (like in that arcade) stereographic perspective is the right one for dome screen. This is extreme example. It gives VR-like experience.
Please Log in or Create an account to join the conversation.
- brussell
Martigen wrote:
Nice! Where's the shader?brussell wrote:
Yes. In short: HudDetected == (Hud1Pixel1 && Hud1Pixel2) || (Hud2Pixel1 && Hud2Pixel2 && Hud2Pixel3 && ...) || ...Martigen wrote: Does it handle multiple 'huds' - i.e difference between a main menu or an in-game inventory? I imagine it depends on the layout of the hud and recognised pixels.
Soon. Next week.
Please Log in or Create an account to join the conversation.
I just yesterday have found huge bug in perspective transformation formula. The perspective which this shader produce is not quite stereographic projection, but still much better than standard linear. Objects at the borders still get distorted, more noticeably in FOV higher than 100 degrees.
The issue is that I based the code on inverted vertex shader that transforms linear projection to stereographic, but pixel UV shaders are not transformational, but look up. Idea can get confusing
But I have good news too. I managed to make new formula that thankfully creates correct distortion correction. But there are still some things to invent.
Like simple UV scaling, for borders management, changes the distortion, because it's look up, not transform.
So tomorrow I will post the geometrical model scheme with detail, and maybe someone will be able to give some help
But hopefully I will be able to figure things out in coming days.
Please Log in or Create an account to join the conversation.
Space can be represented by a sphere, like a Google Street View, where 360 degree image is wrapped on a sphere and seen form inside.
To grab a portion of 3D space (sphere) and display it on a flat surface, like a monitor we have to map its coordinates on flat UV space.
Basically whole topic of map projections is about displaying sphere (world map) or its portion (e.g. city map) on a flat plane.
What we want to achieve here is mapping scaled Stereographic screen coordinates onto Linear image coordinates, since we are using game-texture UV-space lookup.
It has to be scaled at first since we want to adjust the borders size, and scaling (zooming) will change Stereographic screen FOV at the borders of the image.
Simple UV multiply changes the distortion.
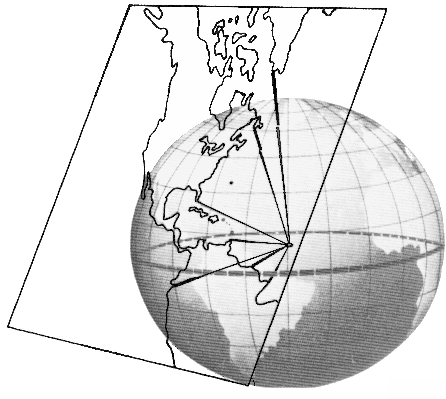
Linear projection in cartography is Gnomonic projection.
And difference between linear projection and stereographic projection is simple point of view.
Linear projection looks from the center of the sphere:
Stereographic projection looks from the surface of the sphere:
Drawing shows flat view from above on the camera frustum.
Even doe it's 2D shader, we operate in 3D space and
only things that we know is UV position of current pixel being processed and in-game camera FOV which user enters in shader settings. That's 2D data, UV = XY, to get the third component Z (XYZ) we can use cotangent of 1/4 FOV.
To get the linear pixel coordinates, we "project" the point onto a sphere surface, then we "look at it" from the sphere center and finally we scale it down to the crosing of the image plane (projection plane).
Now if we scale (zoom) the final image, we also need to scale the Z component, or C component.
The [?=x'/x] is the thing by which we multiply the radial UV coordinates of the game texture.
One can ask, "if it's all cartography, why won't we use already existing formulas!" Well, they're all based on latitude and longitude coordinates which require a lot of trigonometry. We want to avoid that.
It's manageable through similar triangles, etc.
I haven't figure everything out yet, but I'll try. Optimistically I will be able to get new formula in few days, but if you do it faster, feel free.
Please Log in or Create an account to join the conversation.
But some things don't work, maybe somebody can give advice.
Things that work:
- It shows proper stereographic projection.

- You can choose between horizontal, diagonal and vertical FOV
- Manual zooming without deformation

- Changing FOV type, changes distortion alignment, making automatic zoom a problem

- Automatic zooming action to adjust borders
/*
Copyright (c) 2018 Jacob Maximilian Fober
This work is licensed under the Creative Commons
Attribution-ShareAlike 4.0 International License.
To view a copy of this license, visit
http://creativecommons.org/licenses/by-sa/4.0/.
*/
// Perfect Perspective PS ver. 2.0
////////////////////
/////// MENU ///////
////////////////////
uniform float3 Color <
ui_label = "Borders Color";
ui_type = "Color";
> = float3(0.027, 0.027, 0.027);
uniform int FOV <
ui_label = "Field of View";
ui_tooltip = "Match in-game Field of View";
ui_type = "drag";
ui_min = 45; ui_max = 120;
> = 90;
uniform int Type <
ui_label = "Type of FOV";
ui_tooltip = "If image bulges in movement, change it to Diagonal. When proportions are distorted, choose Vertical";
ui_type = "combo";
ui_items = "Horizontal FOV\0Diagonal FOV\0Vertical FOV\0";
> = 0;
uniform int Alignment <
ui_label = "Border Size";
ui_type = "combo";
ui_items = "Optimal Borders\0No Borders\0Full View\0";
> = 0;
uniform float Zooming <
ui_type = "drag";
ui_min = 0.0; ui_max = 10.0; ui_step = 0.001;
> = 1.0;
//////////////////////
/////// SHADER ///////
//////////////////////
#include "ReShade.fxh"
// Stereographic lookup function
// Input is:
// SqrTanFOVq >> squared tangent of quater FOV angle
// Coordinates >> UV coordinates (from -1, to 1), where (0,0) is at the center of the screen
float Function(float SqrTanFOVq, float2 Coordinates)
{
float Result = 1.0 - SqrTanFOVq;
Result /= 1.0 - SqrTanFOVq * (Coordinates.x * Coordinates.x + (Coordinates.y * Coordinates.y));
return Result;
}
// Shader pass
float3 PerfectPerspectivePS(float4 vois : SV_Position, float2 texcoord : TexCoord) : SV_Target
{
// Get Pixel Position
float2 SphCoord = texcoord;
// Get Aspect Ratio
float AspectR = 1.0 / ReShade::AspectRatio;
// Convert FOV type
float FovType = 1.0;
if (Type == 1) // to diagonal
{
FovType = sqrt(AspectR * AspectR + 1.0);
}
else if (Type == 2) // to vertical
{
FovType = AspectR;
}
// Convert 1/4 FOV to radians and calc tangent squared
float SqrTanFOVq = float(FOV) * 0.25;
SqrTanFOVq = radians(SqrTanFOVq);
SqrTanFOVq = tan(SqrTanFOVq);
SqrTanFOVq *= SqrTanFOVq;
// Adjust borders size
float Zoom;
if (Alignment == 0) // Horizontal (Optimal) alignment
{
if (Type == 0) // and Horizontal FOV
{
Zoom = 1.0;
}
else if (Type == 1) // and Diagonal FOV
{
Zoom = 1.0; // needs fix
}
else // and Vertical FOV
{
Zoom = 1.0; // needs fix
}
}
else if (Alignment == 1) // Diagonal alignment
{
if (Type == 0) // and Horizontal FOV
{
Zoom = 1.0; // needs fix
}
else if (Type == 1) // and Diagonal FOV
{
Zoom = 1.0;
}
else // and Vertical FOV
{
Zoom = 1.0; // needs fix
}
}
else // Vertical alignment
{
if (Type == 0) // and Horizontal FOV
{
Zoom = 1.0; // needs fix
}
else if (Type == 1) // and Diagonal FOV
{
Zoom = 1.0; // needs fix
}
else // and Vertical FOV
{
Zoom = 1.0;
}
}
// Convert UV to Radial Coordinates
SphCoord = SphCoord * 2.0 - 1.0;
// Aspect Ratio correction
SphCoord.y *= AspectR;
// Zoom in image and adjust FOV type (pass 1 of 2)
SphCoord *= Zoom * Zooming / FovType;
// SphCoord *= Zooming / FovType;
// Stereographic lookup
SphCoord *= Function(SqrTanFOVq, SphCoord);
// Adjust FOV type (pass 2 of 2)
SphCoord *= FovType;
// Aspect Ratio back to square
SphCoord.y /= AspectR;
// Back to UV Coordinates
SphCoord = SphCoord * 0.5 + 0.5;
// Sample display image
float3 Display = tex2D(ReShade::BackBuffer, SphCoord).rgb;
// Mask out outside-border pixels
if (SphCoord.x < 1.0 && SphCoord.x > 0.0 && SphCoord.y < 1.0 && SphCoord.y > 0.0)
{
return Display;
}
else
{
return Color;
}
}
technique PerfectPerspectiveBeta
{
pass
{
VertexShader = PostProcessVS;
PixelShader = PerfectPerspectivePS;
}
}
Please Log in or Create an account to join the conversation.
It seems that manual zooming is better in some cases, like some games use letter-boxing.
Also anti-aliasing works better when you zoom-out the image few pixels.
Please Log in or Create an account to join the conversation.
- Nanoxo
Please Log in or Create an account to join the conversation.
- Nanoxo
Would it be possible to add a slider to lower the effect intensity linearly from the edges to the center of the screen, in a way that we can keep the same intensity of the effect near the screen edges, but lower the effect intensity near the screen center.
Please Log in or Create an account to join the conversation.
Nanoxo wrote: I'm absolutely loving the effect that this shader had in most of my games while playing in a triple monitor setup, it almost disables the famous "triple screen fish eye effect" perception , but the problem is that the section in the center of the screen (the central monitor) looks a little pixellated and the visibility gets reduced as this section gets "zoomed in".
Would it be possible to add a slider to lower the effect intensity linearly from the edges to the center of the screen, in a way that we can keep the same intensity of the effect near the screen edges, but lower the effect intensity near the screen center.
Zooming is unavoidable, as it is what linear perspective does.
It stretches center of the screen towards infinity when near 180 FOV.
It is possible to zoom out the center screen, but its borders won't be matching with the wing screens.
You would see 2x same things on the center and side monitors.
(...)
Please Log in or Create an account to join the conversation.
The pixelation comes from that. Even VR googles have to deal with it.
For example HTC vive renders game graphics internally at 140% resolution of the display, to compensate for the pixelation - this is one of the reasons why VR games run so slow.
(...)
Please Log in or Create an account to join the conversation.
Let's go deeper
Human can see 180° FOV or more,
we are definitely not using the linear perspective
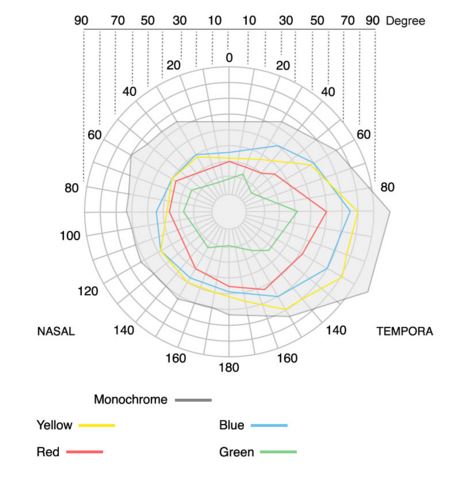
We even see the colors at different FOVs
And check this out:
Source: NASA - Chandra X-Ray Observatory
Cool right?
Please Log in or Create an account to join the conversation.
- Marty McFly
EDIT: Voldemort's binocular vision cone is broader
Please Log in or Create an account to join the conversation.
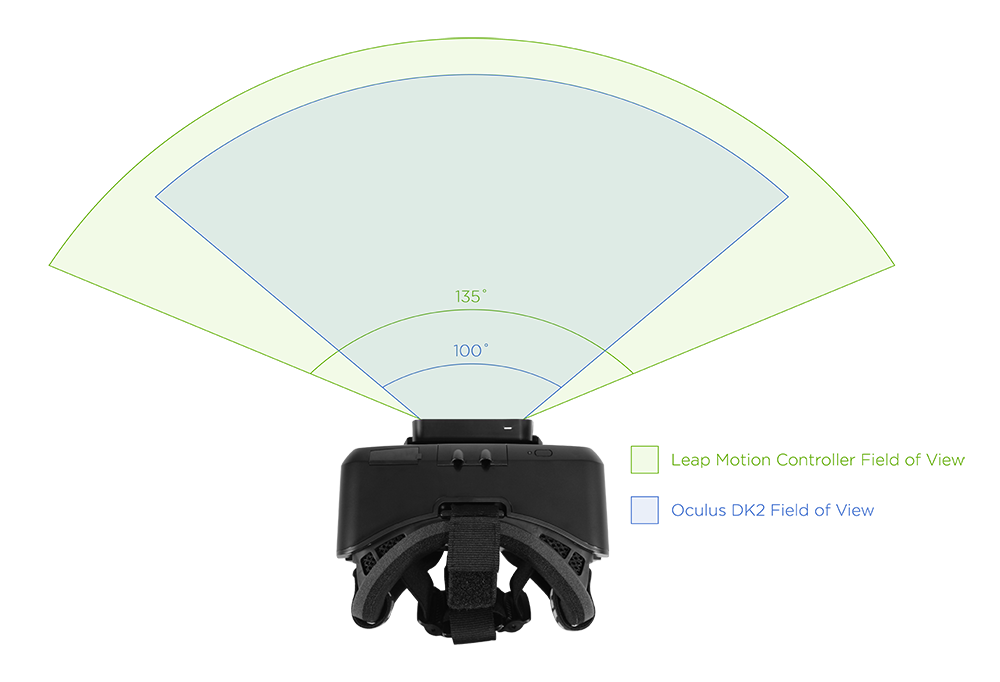
Marty McFly wrote: Is the precise data from the second diagram available somewhere? Would make for an interesting colored vignette filter. Is the the measured difference unidirectional or is it different in top/bottom/left/right?
EDIT: Voldemort's binocular vision cone is broaderno nose blocking the view
Here's the source of the second diagram vr-lens-lab.com/field-of-view-for-virtual-reality-headsets/
Vignette filter like that would be cool. I think YUV space is most human-like. Should be easy to work it out in that space.
In VR, when there's no stationary thing in view, like nose, you get nausea. I wonder if he got some
...This thing would be perfect www.roadtovr.com/nvidia-perceptually-bas...-rendering-research/
if it was available in nvidia control panel
Please Log in or Create an account to join the conversation.
I just updated the PerfectPerspective.fx to version 2.1.2 which addresses the borders issue.Tojkar wrote: (...) I love the old lo-fi monitors, which curves the picture due to their physical properties, but I equally hate the black borders and corners.
I was trying to modify some existing shaders which has the fisheye effect included, but I never managed to succeed. That being said... (...)
It now features texture mirroring, Borders Color now has Alpha channel which blends the borders color with the borders image.
Mirroring borders ON (default) with some color tint works best for motion picture.
Mirroring OFF displays original image at the borders and works nice for screenshoots.
When borders are visible only at the corners, Mirroring ON and Alpha at Zero fixes that.
You can download the updated shader from the official package at github.com/crosire/reshade-shaders
Please Log in or Create an account to join the conversation.
It adds new feature, a vertical distortion amount slider. You can adjust how much vertical lines, like buildings, are distorted.
0 - shows cylindrical stereographic projection
1 - spherical stereographic projection (old behavior)
By default it's set to 0.618 which seems to look nice.
Images:
Please Log in or Create an account to join the conversation.
Available here github.com/crosire/reshade-shaders
Please Log in or Create an account to join the conversation.
- Martigen
Thank you! I use this all the time with Natural Selection 2Fu-Bama wrote: Just released update 2.2.6 adds new ui_category feature from ReShade 3.2.2 and anti-aliasing of image borders.
Available here github.com/crosire/reshade-shaders
Please Log in or Create an account to join the conversation.
- ZapaL
Try and write good or bad.
drive.google.com/open?id=1pRzO5U-NDB1yI8ht3raOjd6nDur_AHTK
https://photos.app.goo.gl/qsQ5Ke5Vq4rweDgz8
https://photos.app.goo.gl/UN75htGqtUFsQDdL9
Please Log in or Create an account to join the conversation.
- Mr. Smiley
This is the project I was referring to: github.com/shaunlebron/blinky
Please Log in or Create an account to join the conversation.